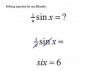gravità/newton/ignoranza e dintorni

[Danybiker88]

No, la resistenza dell'aria e` uguale per entrambi i ciclisti... ma non e` trascurabile.
Se lasciamo cadere un pallone supertela ed una sfera delle stesse dimensioni di piombo pieno, quale delle due arriva prima a terra cadendo da una torre in una giornata senza vento? In questo caso, oltre alla resistenza dell'aria, c'e` anche la spinta di archimede a svantaggio del supertela.
Mi convince molto di piu` questa spiegazione:

No, aspetta, mi sono espresso male allora. Intendevo dire che essendo uguale per entrambi i ciclisti, la possiamo trascurare, ma non che è trascurabile in assoluto, anche perchè sappiamo tutti che senza pedalare e stando seduti si va più piano che stando accovacciati.

Inoltre questo spiega i miei dati sperimentali, ovvero che anche in bici da corsa su una discesa liscia come un tavolo da biliardo il ciclista piu` pesante (io) andava piu` veloce rispetto al cilcista piu` leggero. Le bici erano praticamente identiche.

Eh, ma guarda che sul piano inclinato, in assenza di attriti, la velocità finale è indipendente dalla massa del corpo.

Tratto da wiki "Altra importante scoperta fatta da Galilei con gli esperimenti sul piano inclinato è la legge di conservazione dell'energia: notò infatti che il moto (in particolare la velocità) della sfera lungo il piano è indipendente dalla massa della sfera stessa"

Non a caso l'equazione del moto di un corpo sul piano inclinato in assenza di attrito è:

in cui non rientra la massa.
D'altronde se g è uguale per tutti i corpi, anche la sua risultante sul piano inclinato (ovvero l'accelerazione del corpo) è la medesima indipendentemente dalla massa.

Se a questo aggiungi che gli attriti (attrito ai perni e attrito gomma asfalto) sono proporzionali al peso (quindi aumentano con l'aumentare del peso) capisci che è impossibile che, anche su un fondo liscio (dove gli attriti influiscono di meno) il ciclista più pesante vada più forte!

Prodotti MTB scontati

 

[shrdlu]

No, aspetta, mi sono espresso male allora. Intendevo dire che essendo uguale per entrambi i ciclisti, la possiamo trascurare, ma non che è trascurabile in assoluto, anche perchè sappiamo tutti che senza pedalare e stando seduti si va più piano che stando accovacciati.

No, non la puoi trascurare, non puoi dire che ignori due forze perche` sono uguali se poi dall'altra parte parli di accelerazioni costanti. Due corpi di massa diversa che hanno la stessa accelerazione sono sottoposti a forze diverse. O ragioniamo in Newton o ragioniamo in m/s2...
La forza derivante dalla resistenza aerodinamica e` indipendente dal peso, quindi l'accelerazione (o meglio, la decelerazione) derivante dalla resistenza aerodinamica e` superiore per il ciclista piu` leggero.
L'accelerazione di gravita` invece e` la stessa.
Se i due corpi partono dalla stessa velocita` in caduta libera (o su un piano inclinato in assenza di altri attriti), il corpo piu` pesante e` soggetto ad una accelerazione risultante verso il basso superiore. All'istante t = T0 + dt, quale dei due andra` piu` veloce? Ovviamente la sfera di piombo piena, non certo il supertela.
I link di bis e Ser Pecora sviluppano questo concetto in modo piu` formale.

(...) capisci che è impossibile che, anche su un fondo liscio (dove gli attriti influiscono di meno) il ciclista più pesante vada più forte!

...questo pero` non concorda con l'evidenza sperimentale, a meno che sulla discesa dall'eremo con l'asfalto appena rifatto non valgano leggi fisiche locali diverse dal resto dell'universo.

 

[bis]

No, aspetta, mi sono espresso male allora. Intendevo dire che essendo uguale per entrambi i ciclisti, la possiamo trascurare, ma non che è trascurabile in assoluto, anche perchè sappiamo tutti che senza pedalare e stando seduti si va più piano che stando accovacciati.

Mi sa che non puoi trascurarla visto che nella caduta dei gravi, a parita' di superficie esposta, il corpo piu' pesante va piu' forte.

 

[bis]

Eh, ma guarda che sul piano inclinato, in assenza di attriti, la velocità finale è indipendente dalla massa del corpo.

Mi sa che questa cosa e' vera in assenza di aria (sempre attrito e').
Per l'attrito col piano, invece, quel che succede a due corpi di massa diversa con stesso coefficiente d'attrito, e' che cambiando l'inclinazione del piano iniziano a muoversi contemporaneamente quando il coefficiente d'attrito eguaglia il valore della tangente dell'angolo d'inclinazione - (a prescindere quindi dalla massa).

 

[Danybiker88]

Effettivamente avete ragione...
Ho trovato un sito in cui ci sono i parametri di coefficiente aereodinamico e sezione frontale di un ciclista. Facciamo due calcoli. Il prodotto SCx vale 0,2 m2.

- A 40km/h quindi otteniamo che la resistenza aereodinamica è di -192N.

- Calcoliamo il contributo della pendenza per un ciclista di 60kg e di uno di 100kg. Supponiamo di trovarci su una pendenza del 20% => θ=11,3°.
La formula per calcolare la resistenza dovuta alla pendenza (in questo caso è un contributo) è: Rp=P*tgθ= P*tg11,3°
Ciclista da 100kg (=981N): Rp=981*tg11,3°=196N
Ciclista da 60kg (=588N): Rp=588*tg11,3°=118N

- La resistenza ai perni è praticamente uguale per i due ciclisti e per di più molto piccola, quindi la trascuriamo.

- Calcoliamo ora la resistenza al rotolamento. Visto che i nostri amici bitumari hanno fatto dei test a proposito, supponiamo di essere in BDC. ATTENZIONE: l'attrito di una copertura da bici da corsa non è minimamente paragonabile a quello di una copertura da MTB, quindi il contributo nel nostro caso sarà nettamente maggiore! Purtroppo però non ci sono test di questo tipo su coperture MTB... Se trovate i coefficienti di resistenza al rotolamento (Crr) di coperture da MTB, linkate.

Prendiamo le Tufo Hi-Comp Carbon come riferimento (le coperture da strada con Crr più alto): Crr= 0.0077 a 7 bar.


Calcoliamo la resistenza al rotolamento per i due ciclisti:
Ciclista da 100kg (=981N): Rrr=981*0.0077=7.55N
Ciclista da 60kg (=588N): Rrr=588*0.0077=4.53N

Applicando l'equazione della trazione (somma di tutte le resistenze):

------ ERRORE ------ Ho considerato il contributo di una sola ruota

Ciclista da 100kg: F=196-192-7.55=-3,55N
Ciclista da 60kg: F=118-192-4.53=-78,53N

Con la differenza di 74,98N (valido per ciclista su bici da corsa).
---------------------

-----CORREZIONE------
Ciclista da 100kg: F=196-192-2*7.55=-11,1N
Ciclista da 60kg: F=118-192-2*4.53=-83,06N

Con la differenza di 71,96N (valido per ciclista su bici da corsa).
-----------------------
Considerazioni: è interessante notare come per il ciclista da 100kg la resistenza al rotolamento sia del 166% quella del ciclista da 60kg. I risultati di questo calcolo valgono solo in Bdc. Il coefficiente di attrito delle Bdc è bassissimo. Poichè il Crr dei copertoni da MTB è più alto, la resistenza al rotolamento diventa molto più influente in MTB.
Ho il sospetto che la situazione per la MTB si possa invertire!

 

[ADexu]

Se nel frattempo qualcuno volesse trastullarsi con qualche calcoletto: http://www.analyticcycling.com/ForcesSource_Page.html

Per delle gomme da MTB i Crr dovrebbe aggirarsi intorno a 0.008/0.012 a seconda della sezione e della tassellatura

 

[tettabeta]

D'altronde anche dall'esperienza comune sappiamo che su un percorso ricco di ostacoli medio piccoli (radici, pietre) con la gomma gonfissima la bici avrà difficoltà a superare l'ostacolo e specialmente il manubrio sarà soggetto a maggiori sollecitazioni (movimenti vertivali), mentre con una pressione più bassa la marcia risulterà più fluida e le sollecitazioni verticali inferiori.

Punti da ponderare:

1) L'assorbimento urti da parte di una gomma e' un lavoro, ovvero energia impiegata per deformare la gomma e comprimere l'aria al suo interno

2) E le sospensioni ?

3) omissis

4) Ruota gonfissima che non supera l'ostacolo, piu' sgonfia lo supera: dissento. La ruota sgonfia offre un raggio minore di "rotolamento", mentre quella gonfiata "dura" offrira' quei 2-3 cm di diametro che in situazioni critiche possono fare la differenza tra il capottone e lo scampato pericolo

5) Il peso del conducente "ciccio" e' tutta inerzia che aiuta a "galleggiare" sugli ostacoli, mentre la leggerezza del conducente "esile" lo fa saltellare sugli ostacoli, utilizzando quindi dell'energia per inutili accellerazioni verticali.


Data una mucca semisferica di raggio 12,
(o )Beta

 

[Ser pecora]

data una mucca semisferica di raggio 12,
(o )beta

qed

 

[essetierre]

Effettivamente avete ragione...
Ho trovato un sito in cui ci sono i parametri di coefficiente aereodinamico e sezione frontale di un ciclista. Facciamo due calcoli. Il prodotto SCx vale 0,2 m2.

- A 40km/h quindi otteniamo che la resistenza aereodinamica è di -192N.

- Calcoliamo il contributo della pendenza per un ciclista di 60kg e di uno di 100kg. Supponiamo di trovarci su una pendenza del 20% => θ=11,3°.
La formula per calcolare la resistenza dovuta alla pendenza (in questo caso è un contributo) è: Rp=P*tgθ= P*tg11,3°
Ciclista da 100kg (=981N): Rp=981*tg11,3°=196N
Ciclista da 60kg (=588N): Rp=588*tg11,3°=118N

- La resistenza ai perni è praticamente uguale per i due ciclisti e per di più molto piccola, quindi la trascuriamo.

- Calcoliamo ora la resistenza al rotolamento. Visto che i nostri amici bitumari hanno fatto dei test a proposito, supponiamo di essere in BDC. ATTENZIONE: l'attrito di una copertura da bici da corsa non è minimamente paragonabile a quello di una copertura da MTB, quindi il contributo nel nostro caso sarà nettamente maggiore! Purtroppo però non ci sono test di questo tipo su coperture MTB... Se trovate i coefficienti di resistenza al rotolamento (Crr) di coperture da MTB, linkate.

Prendiamo le Tufo Hi-Comp Carbon come riferimento (le coperture da strada con Crr più alto): Crr= 0.0077 a 7 bar.

Calcoliamo la resistenza al rotolamento per i due ciclisti:
Ciclista da 100kg (=981N): Rrr=981*0.0077=7.55N
Ciclista da 60kg (=588N): Rrr=588*0.0077=4.53N

Applicando l'equazione della trazione (somma di tutte le resistenze):

Ciclista da 100kg: F=196-192-7.55=-3,55N
Ciclista da 60kg: F=118-192-4.53=-78,53N

Con la differenza di 74,98N (valido per ciclista su bici da corsa).

Considerazioni: è interessante notare come per il ciclista da 100kg la resistenza al rotolamento sia del 166% quella del ciclista da 60kg. I risultati di questo calcolo valgono solo in Bdc. Il coefficiente di attrito delle Bdc è bassissimo. Poichè il Crr dei copertoni da MTB è più alto, la resistenza al rotolamento diventa molto più influente in MTB.
Ho il sospetto che la situazione per la MTB si possa invertire!

OT:
1) Scusa ma nel contributo dovuto alla pendenza non ci dovrebbe essere un seno invece che la tangente (dalla trigonometria...)?

2) Nel calcolo della perdita dovuta all' attrito di rotolamento ti sei dimenticato di considerare il fatto che il piano è inclinato quindi non grava tutto il peso sulla ruota, ma una sua componente (coseno di teta...). In verità neanche questo è vero perchè il peso del pilota, durante una discesa si sposta "in qua e in la"... Se la discesa è sconnessa, poi, il rimbalzo fa si che il peso che agisce sulle ruote vari da momento a momento e quindi è pressoche impossibile considerare un valore costante (a meno di fare una media...)... Soprattutto se si lavora con numeri, visti quelli dell'attrito volvente (o di rotolamento) cosi' piccoli...

3)Le ruote sono 2

Dimmi se sbaglio

 

[essetierre]

qed

hahahahaha!!!!!!!!!!!!!!!!!!!!!!

 

[essetierre]

Punti da guardare per risolvere questo dilemma (o quello che contano di piu')....

1)Forza dovuta al peso del pilota (contributo energetico)

2)Forza della molla forcella e (se c'e') ammo (perdita energetica)moooooollltttto difficile da calcolare....

3) attrito di rotolamento (o volvente) (perdita energetica)

4) Attriti vari dovuti a cuscinetti, coppie rotoidali varie (perdita energetica)

5)Resistenza dell'aria (perdita energetica)

6)Perdite dovute a disconnessioni del terreno (radici, buche....)


Se qualcuno si vuole cimentare nelle relazioni matematiche....

 

[bis]

OT:
1) Scusa ma nel contributo dovuto alla pendenza non ci dovrebbe essere un seno invece che la tangente (dalla trigonometria...)?

c'e' un seno diviso per un coseno .. quindi una tangente.
La forza parallela al piano inclinato e' il seno e la forza perpendicolare a questa e' il coseno.

 

[essetierre]

c'e' un seno diviso per un coseno .. quindi una tangente.
La forza parallela al piano inclinato e' il seno e la forza perpendicolare a questa e' il coseno.

E allora? io voglio trovare la componente parallela al piano (mg seno di teta), quella che mi spinge giu dal piano...

Di quella perpendicolare al piano non mi interessa nulla ai fini del contributo della forza peso...

Non capisco perche dividete il seno con il coseno per trovare la tangente...

 

[bis]

E allora? io voglio trovare la componente parallela al piano (mg seno di teta), quella che mi spinge giu dal piano...

Di quella perpendicolare al piano non mi interessa nulla ai fini del contributo della forza peso...

Non capisco perche dividete il seno con il coseno per trovare la tangente...

Ora che mi fai notare c'e' qualcosa che non torna neppure a me - non capisco perche' moltiplica il peso per il coefficiente d'attrito.
Il coefficiente d'attrito si calcola eguagliando la forza parallela al piano inclinato con una forza di verso opposto dovuta appunto all'attrito.
in pratica:
la forza in discesa e' F=Peso x seno di teta
l'opposta e' R= K * Peso x coseno di teta
eguagliando F a R si ottiene che K = perso x seno di teta/ peso x coseno di teta.. da cui K (coefficiente d'attrito) = tangente di teta.

 

[essetierre]

Ora che mi fai notare c'e' qualcosa che non torna neppure a me - non capisco perche' moltiplica il peso per il coefficiente d'attrito.
Il coefficiente d'attrito si calcola eguagliando la forza parallela al piano inclinato con una forza di verso opposto dovuta appunto all'attrito.
in pratica:
la forza in discesa e' F=Peso x seno di teta
l'opposta e' R= K * Peso x coseno di teta
eguagliando F a R si ottiene che K = perso x seno di teta/ peso x coseno di teta.. da cui K (coefficiente d'attrito) = tangente di teta.

Lui moltiplica il peso (sbagliato perche avrebbe dovuto considerare soltanto la parte della forza peso perpendicolare al piano di appoggio) per il coeff. di attrito volvente perche cosi trova la forza che si oppone al moto dovuta al rotolamento della ruota.

Dai miei studi (universitari) l'attrito volvente funziona cosi: (seguimi)

Quando un corpo si muove di moto rotatorio ed e' soggetto ad una forza che lo schiaccia al suolo (in questo caso il peso dovuto alla massa del pilota e della bici), il corpo si deforma (tutti i corpi nella realta'), nasce per vari motivi (tralasciamo questo particolare ma sono in generale legate a perdite energetiche dovute ad attriti interni e alla perfetta non elasticita dei corpi reali), un momento che tende a far rallentare il corpo.

La forza di attrito volvente (quella che si oppone al moto) si trova:

F= mg*(coeff di attr. volvente)

Lui il coeff. di attrito ce l'ha di gia e l'ha moltiplicato per il peso trovando cosi la forza che si oppone al moto di discesa della mtb dovuto al rotolamento delle ruote, ma questo è sbagliato per tre ragioni:

1) come gia detto non ha considerato soltanto la componente perpendicolare al terreno...

2) Le ruote sono due quindi la perdita energetica dovuta alle ruote va rivista

3) E' pressoche impossibile stimare precisamente le perdite energetiche dovute al rotolamento perche: il peso che agisce sulle ruote varia troppo nel tempo e perche il peso del corpo, spostandosi non è mai costante... in piu se il terreno è sconnesso ogni volta che la ruota riatterra intervengono delle forze dette forze impulsive che fanno "impennare" il peso che agisce sulla ruota e quindi la forza d'attrito... (come si fa a sapere quando precisamente intervengono tali forze?). Per le BDC tutti i calcoli sono piu semplici perche tutto è piu lineare (dall'asfalto alle forze che agiscono sulle ruote...).


Tuttavia ritengo, che pur avendo fatto questi errori che a livello concettuale sono gravi, non sia andato poi cosi lontano dalla soluzione giusta ( soprattutto accettabile ) perchè ad un angolo cosi "piccolo" :

A) Tangente e seno (per il calcolo della forza peso parallela al piano) quasi coincidono

B) Il coseno (utile per il calcolo della forza resistente di rotolamento) è pressoche 1...

Che ne pensi?

 

[bis]

Lui moltiplica il peso (sbagliato perche avrebbe dovuto considerare soltanto la parte della forza peso perpendicolare al piano di appoggio) per il coeff. di attrito volvente perche cosi trova la forza che si oppone al moto dovuta al rotolamento della ruota.

Dai miei studi (universitari) l'attrito volvente funziona cosi: (seguimi)

Quando un corpo si muove di moto rotatorio ed e' soggetto ad una forza che lo schiaccia al suolo (in questo caso il peso dovuto alla massa del pilota e della bici), il corpo si deforma (tutti i corpi nella realta'), nasce per vari motivi (tralasciamo questo particolare ma sono in generale legate a perdite energetiche dovute ad attriti interni e alla perfetta non elasticita dei corpi reali), un momento che tende a far rallentare il corpo.

La forza di attrito volvente (quella che si oppone al moto) si trova:

F= mg*(coeff di attr. volvente)

Lui il coeff. di attrito ce l'ha di gia e l'ha moltiplicato per il peso trovando cosi la forza che si oppone al moto di discesa della mtb dovuto al rotolamento delle ruote, ma questo è sbagliato per tre ragioni:

1) come gia detto non ha considerato soltanto la componente perpendicolare al terreno...

2) Le ruote sono due quindi la perdita energetica dovuta alle ruote va rivista

3) E' pressoche impossibile stimare precisamente le perdite energetiche dovute al rotolamento perche: il peso che agisce sulle ruote varia troppo nel tempo e perche il peso del corpo, spostandosi non è mai costante... in piu se il terreno è sconnesso ogni volta che la ruota riatterra intervengono delle forze dette forze impulsive che fanno "impennare" il peso che agisce sulla ruota e quindi la forza d'attrito... (come si fa a sapere quando precisamente intervengono tali forze?). Per le BDC tutti i calcoli sono piu semplici perche tutto è piu lineare (dall'asfalto alle forze che agiscono sulle ruote...).


Tuttavia ritengo, che pur avendo fatto questi errori che a livello concettuale sono gravi, non sia andato poi cosi lontano dalla soluzione giusta ( soprattutto accettabile ) perchè ad un angolo cosi "piccolo" :

A) Tangente e seno (per il calcolo della forza peso parallela al piano) quasi coincidono

B) Il coseno (utile per il calcolo della forza resistente di rotolamento) è pressoche 1...

Che ne pensi?

Si, come dici tu la formula per la forza di attrito volvente deve considerare la perpendicolare quindi:
F = mg*cosθ*(coeff. attrito volvente) e .. visto che l'attrito volvente e' pari a tanθ.. alla fine si ha F=mg*senθ.
Senθ che quindi identifica la forza con direzione parallela al piano.
Son d'accordo anche sul resto ...

 

[luppolo]

mamma mia quanto la fate lunga!!!...basta con l'approccio "accademico", e sposiamo l'approccio ingegneristico!!!

...ok..ci sono gli attriti, il rotolamento , i mozzi l'aria ecc ecc...ma la componente "forza peso" è predominante nel problema posto (e...sinceramente , in generale...a meno di indossare un giubbetto a modo di vela!)!

detto , accademicamente, tutte le altre forze che si oppongono al moto sono di molti ordini i grandezza inferiori, e quindi possono tranquillamente nn essere considerati!

quindi...la risposta al quesito è ... in generale, "il piu' pesante va' piu' forte"....

la teoria è bene saperla...ma poi per lavorare e progettare si devono fare delle ipotesi semplificative, altrimenti nn nè venite piu' fuori!..e bisogna imparare a leggere bene cio' che si chiede!

lui ha detto "in condizioni simili, perchè io piu' pesante vado piu' forte di lui piu leggero'" e la risposta come detto è semplicissima, come gia' detto sopra!..problema risolto

diverso era se si chiedeva "perchè a parita di peso , con bici SIMILI, ma nn IDENTICHE, uno va' piu' forte dell'altro?"...beh, allora potevate dilettarvi con l'accademia...

 

[Danybiker88]

Tuttavia ritengo, che pur avendo fatto questi errori che a livello concettuale sono gravi, non sia andato poi cosi lontano dalla soluzione giusta ( soprattutto accettabile ) perchè ad un angolo cosi "piccolo" :

A) Tangente e seno (per il calcolo della forza peso parallela al piano) quasi coincidono

B) Il coseno (utile per il calcolo della forza resistente di rotolamento) è pressoche 1...

Che ne pensi?

Rispondo per precisare che quelli che hai identificato come errori, sono in realtà delle semplici approssimazioni che si applicano nel campo dell'ingegneria stradale.
Parlando infatti di pendenze di strade, nel nostro caso 20% (una pendenza non da poco, la massima in cui si posso applicare tali approssimazioni) si possono fare delle approssimazioni del tipo considerare il vettore forza peso verticale e non la sola componente normale alla superficie strada (Pcosθ), così come nel calcolo del contributo della pendenza per angoli fino a 10° si può approssimare sinθ con tgθ, essendo l'errore trascurabile.

Nel caso specifico poi l'obiettivo è di dare una stima, non ci interessa calcolare al decimo di N le forze! Si tratta di un'applicazione pratica e parametri come il coefficiente di resistenza al rotolamento sono parametri sperimentali. L'errore che si ottiene quindi è inferiore alla precisione che interessa avere e quindi tali approssimazioni sono giustificabili.

Sul fatto di aver considerato invece una sola ruota hai ragione: errore di distrazione!

 

[shrdlu]

...ok..ci sono gli attriti, il rotolamento , i mozzi l'aria ecc ecc...ma la componente "forza peso" è predominante nel problema posto (e...sinceramente , in generale...a meno di indossare un giubbetto a modo di vela!)!

detto , accademicamente, tutte le altre forze che si oppongono al moto sono di molti ordini i grandezza inferiori, e quindi possono tranquillamente nn essere considerati!

quindi...la risposta al quesito è ... in generale, "il piu' pesante va' piu' forte"....

Ci sono tre ipotesi:

1 - Stai scherzando vero?

2 - Sei un ingegnere gestionale.

3 - Sei un ingegnere gestionale laureato alla CEPU.

 

[tettabeta]

mamma mia quanto la fate lunga!!!...basta con l'approccio "accademico", e sposiamo l'approccio ingegneristico!!!

Non so se darti una reputa poisitiva, o una negativa.

1) Solitamente diffido degli ingegneri.

2) Solitamente diffido degli accademici

3) Solitamente stimo chi applica sul campo le proprie convinzioni

4) Farla lunga e' la ragione d'essere del forum. (es.: "Che cos'e' il freeride ? " )

5) Io sono gia' sposato

6) Tutta questo 3d sortisce dal fatto CHE SI VUOLE DIMOSTRARE teoricamente che il piu' pesante scende piu' veloce.

7) Progettare: siamo tutti progettisti un po' come nel pallone sono tutti C.T.

8) Il tuo nick evoca piacevoli abitudini

9)

diverso era se si chiedeva "perchè a parita di peso , con bici SIMILI, ma nn IDENTICHE, uno va' piu' forte dell'altro?"...beh, allora potevate dilettarvi con l'accademia...

..che e' piu' o meno la premessa di questa discussione (come postulato da Adexu). O no ?

Piis en lov,
(o )Beta