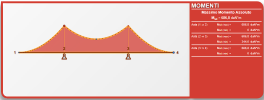
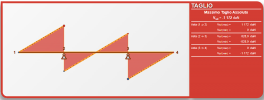
Non so, mi sembra che stai facendo dei calcoli sbagliati. Ora hai corretto a 0,207 che è abbastanza vicino a 2/9 (0,222), ma la formula sembra scritta errata: radq(2) / 2(1+radq(2)) = 0,293 circa, e non 0.207
Prima avevi scritto: "... é a circa 0.317 volte L dal bordo. Per la precisione, a radq(3) / 2(1+radq(3))".
Marika, sei molto brava! Non sto mettendo in dubbio nulla, ma dovresti rivedere la procedura, provando a fare un ragionamento logico, legandolo ad un esperimento pratico.
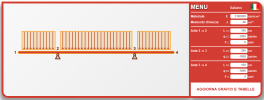
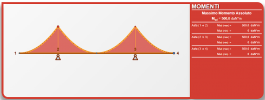
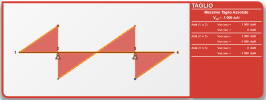
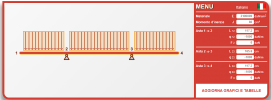
Prendi un manico di scopa o qualcosa di simile che sia uniforme (va bene anche un tubo di ferro di 1 metro) e segna i 2/9 esterni, poi sorreggi il manico in quei due punti con sole due dita per punto. Fai colpire il manico da una terza mano, in modo che entri in risonanza. Ascolta sia le vibrazioni meccaniche che quelle acustiche. Ebbene, quella frequenza è la nota più bassa che quel pezzo di legno possa suonare. I 2/9 sono i nodi di vibrazione che corrispondono alla semi-lunghezza d'onda (5), per cui lambda è 10 (1+9), e determinano i punti di appoggio migliori di qualsiasi mensola (o, campata con due sbalzi simmetrici).
Prova a partire da questo precetto, e se sei in grado di farlo, potresti anche trovare la formula teorico-matematica che conferma la realtà: in questo caso 2/9 o un numero molto molto vicino (già 0,207 mi sembra troppo lontano).
Tu prova ad aprire un libro di scienza delle costruzioni.
La prima variante è perchè avevo fatto i conti al volo... un banale errore algebrico.
Grazie per avermelo segnalato. Effettivamente è 0.293 L.
PS: la trave é isostatica